Creating a recursive dynamic method that calculates factorial

Posted by Filip Ekberg on 17 Oct 2011

In the last post we looked at how we could call a dynamic method, now let's have a look at how we can create a recursive method that calculates factorial for non-negative integers! First of all we should take a look at what factorial means, usually it's written like this:

5!

Which means that it will perform this:

5*4*3*2*1

So by looking at the above sequence we can see that we want to perform the multiplication operation over and over again, reducing the integer by 1 until it's equal to one. Here's a good explanation if you don't know what recursion is:

Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion.

If you are having troubles understanding what recursion is, start by reading this blog post from the beginning again. When talking about recursion, you look for one or more base cases, these are the times that the recursion ends. In the above, the base case is when the integer has been reduced to 1.

Let's start off by looking at the method signature here, the method will return an integer and take an integer as its first argument:

int Factorial(int x)

Then we want to define our base base, which in this case will be when x is equal to 1, then we want to end the recursion and return x:

if (x == 1) return x;

The last part is a bit tricky to understand, what we want to do is that we want to multiply x with the value of Factorial(x-1) this means that if we call Factorial(3) we expect the following to happen the first time:

return 3*Factorial(3 - 1);

In this case, we will call the method with the value 2 and then the return-statement will look like this:

return 2*Factorial(2 - 1);

But now when we're inside Factorial this time, x will be equal to 1, so we will return 1, which means that we will actually multiply 2 by 1 and then we return that value and we will return 3 by 2.

This is the entire recursive method that we want to produce as a dynamic method:

int Factorial(int x)
{
    if (x == 1) return x;
    return x*Factorial(x - 1);
}

Just as we've done in the previous posts, we instantiate our DynamicMethod like this:

Type[] methodArguments = { 
    typeof(int)
};

var recursiveFactorial = new DynamicMethod(
        "Factorial",
        typeof(int),
        methodArguments,
        typeof(Program).Module);

var il = recursiveFactorial.GetILGenerator();

As you can see here we expect one parameter and that is an integer and we expect a return value which will be an integer as well. Now, there is one new operation code that we are going to look on today and there are two other methods on the il-generator that we will explore. First of all we need to look at how we can create an if-statement and jump to somewhere in the code.

Basically what an if-statement does is that it evaluates if two values conform to a certain rule, it might be equality or not-equality among others and then it tells you to go somewhere, either you enter the body or you continue after the body of the if-statement.

When we look at IL it's not so different, but at a first glance it might look like that. So first of all, we need to be able to define somewhere where we will go if our statement is true, this is done by calling DefineLabel() on our il-generator instance like this:

var endOfMethod = il.DefineLabel();

This will give us an instance of the class Label and if you've not seen labels before in any programming languages, it might look like this:

someLabel:
    Console.WriteLine("Goto test");
goto someLabel;

A more common scenario might be if you have nested loops, which might not be a good idea in the long term anyways but if you do, using labels will allow you to break the outer loop. In our case on the other hand, we will use the label to jump somewhere when our check evaluates to true. Evaluating if two values are equal is done by using the operation code OpCodes.Beq. It will assume that two values are pushed onto the evaluation stack and if they are equal, it will jump to the label that you've emitted with the operation code. Like this:

il.Emit(OpCodes.Beq, endOfMethod);

This will jump to wherever endOfMethod is if the two values on the evaluation stack are equal. So now that we've covered almost all of the new things, let's get rocking with some more IL!

The first thing that I want to do when my method enters, is reading the value passed to my method, this is because I want to use this method later on.

The second thing is to check if the parameter is equal to one, however the branch-is-equal operation will pop the two values from the evaluation stack, so in order for us not to lose our value passed to our method, we just push it onto the stack again, we also push the value 1 because that's what we want to evaluate against and the stack will look something like this now:

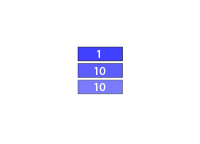
Which means that after we've done:

il.Emit(OpCodes.Beq, endOfMethod);

It will look like this:

We haven't defined where endOfMethod is yet, we just have the label for usage. So the next thing we want to emit is what happens if the branch did not work and this is the subtraction. This assumes that we have two values on the evaluation stack as well, so we just need to push the value 1, which is what we want to subtract with:

il.Emit(OpCodes.Ldc_I4, 1);

So now the stack looks like this:

The next thing we do is to actually call the subtraction:

il.Emit(OpCodes.Sub);

This will pop the two values off the stack and push the result so the stack will look like this:

When the subtraction is done, we want to call the method recursively and to do this, we just call our own dynamic method and since we have the result from the subtraction on the evaluation stack, this will be treated as the first argument to the method:

il.Emit(OpCodes.Call, recursiveFactorial);

The code after this is where we are when the method actually returns and here we want to multiply the return value by the argument that we first sent to our method, the return value from the method is already on the evaluation stack, so we just need to add the argument again and call the multiplication operation:

il.Emit(OpCodes.Ldarg_0);
il.Emit(OpCodes.Mul);

Everything above up until where we did the branch is when the base case did not fall through now we need to define the entry point for the end of our method, which means that we have to mark where the label should be. This is how we do that:

il.MarkLabel(endOfMethod);

However, both the base case and every time this method is called have a similar ending and that is returning a value, the value will always be on the evaluation stack either if it's from the multiplication above, or if it is from the subtraction even further up:

il.Emit(OpCodes.Ret);

This is the entire il that I emitted:

// Either to return or send as argument to recursive call
il.Emit(OpCodes.Ldarg_0);

// Compare the argument value to 1
il.Emit(OpCodes.Ldarg_0);
il.Emit(OpCodes.Ldc_I4, 1);
// Jump to endOfMethod if the argument value is equal to 1
il.Emit(OpCodes.Beq, endOfMethod);

// Subtract 1
il.Emit(OpCodes.Ldc_I4, 1);
il.Emit(OpCodes.Sub);

// Do recursive call
il.Emit(OpCodes.Call, recursiveFactorial);

// Multiply the return value by the argument value
il.Emit(OpCodes.Ldarg_0);
il.Emit(OpCodes.Mul);

il.MarkLabel(endOfMethod);
il.Emit(OpCodes.Ret);

To try it out, we can call it like this:

var toInvoke = (Func<int, int>)recursiveFactorial.CreateDelegate(typeof(Func<int, int>));
var fact = toInvoke(10);

And this is the result:

I hope you found this interesting because I had a lot of fun writing it and if you have any thoughts please leave a comment below!

Follow @fekberg